East Level 2
Well-Known Member
Easy to explain.What about the little bit that’s missing? Where is it?!?
If you have a cake and cut it into thirds you have 33.3% in each slice. So three slices add up to 99.9% and the missing 0.1% is on the knife.
Easy to explain.What about the little bit that’s missing? Where is it?!?
Yes, because it has the same number of multiplied equivalent fractions (as many as you can be arsed with) and can also have 2/3.Are there some fractions that have more equivalent fractions? The fact you can simply double and keep doubling every fraction would seem to indicate every fraction has an infinite number of equivalent fractions I.e 2/3 = 4/6 = 8/12
3/7 = 6/14 = 12/28 etc etc
But what about fractions that you can also divide to get a equivalent fraction:
4/6 = 8/12 = 16/24 etc etc ad infinitum but also 4/6 = 2/3
So does 4/6 have more equivalent fractions than 3/7?
That’s what I think but how can you have more than infinity?!?Yes, because it has the same number of multiplied equivalent fractions (as many as you can be arsed with) and can also have 2/3.
Some infinity’s are bigger than others.That’s what I think but how can you have more than infinity?!?
This is my kind of Maths.5318008 = BOOBIES
And looks like an ass...marvelous!Finished my online course. Usually graphs are rectangular i.e. y vs x but in the graph below, I have plotted the variable r against x in polar coordinates to produce a 'cardioid'.
At x = 0 degrees r=1, and at x=90 degrees, r=0, at x=270 degrees, r = -2.
This shapes follows from the sine wave and its symmetry around it peak at pi/2.
View attachment 168987
My ERO would say so but it's rock solid optical fibre whatnot broadband!SEVEN YEARS to comment on my post?
Are you still using a dial up modem?
Until you reach the Trump infinity. Nothing bigger or betterSome infinity’s are bigger than others.
Couldn't work it out in 5 minutes so I googled the solution.Twelve golf balls each numbered 1-12.
At point of commencement, any one of the balls can be either lighter or heavier than the other eleven.
Using a set of balance scales, in three moves, determine the number of the ball and its difference to the others
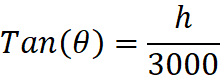
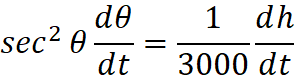
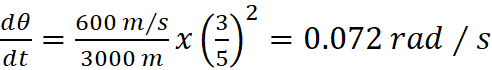 or 4.13⁰/ s
or 4.13⁰/ sI came across a nice problem that using implicit differentation. The source for it is
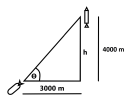
A rocket blasts off vertically from a flat surface. You are 3000m from the rocket at launch and you have a ground-based camera. At a height of 4000m, you need to know what is the rate of change of inclination of your camera to keep it in your field of view. The rocket is assumed to be travelling vertically and has a velocity of 600 m/s at 4000m.
We can define a triangle as below and make the relation: View attachment 174085
Using implicit differentiation, we can differentiate both sides with respect to time, t…
View attachment 174082
View attachment 174084
secϴ= 1/cos = 5/3, and dh/dt = 600 m/s.
Rearranging, we get View attachment 174083 or 4.13⁰/ s
